
Naukowcy poczynili znaczny postęp w geometrii spektroskopowej, udowadniając szczególny przypadek hipotezy Bolyi dotyczącej wartości własnych dysku. Ich praca, łącząca teoretyczną elegancję z potencjalnymi zastosowaniami praktycznymi, podkreśla uniwersalną wartość i artystyczne piękno badań matematycznych. Źródło: SciTechDaily.com
Jeden z profesorów i jego współpracownicy udowodnili przypuszczenie Polyi o wartościach własnych dysku, trudnym problemie matematycznym.
Czy na podstawie dźwięków, jakie wydaje, można wywnioskować kształt bębna?
Takie pytania lubi zadawać Iosif Poltrovic, profesor na Wydziale Matematyki i Statystyki Uniwersytetu w Montrealu. Poltrovic wykorzystuje geometrię spektroskopową, dział matematyki, do zrozumienia zjawisk fizycznych związanych z rozchodzeniem się fal.
Przełom w estymacji matematycznej
Zeszłego lata Poltrović i jego międzynarodowi współpracownicy – Nikołaj Filonow, Michael Levitin i David Scherr – udowodnili szczególny przypadek słynnej hipotezy o geometrii spektroskopowej sformułowanej w 1954 roku przez wybitnego węgiersko-amerykańskiego matematyka George'a Polyę.
Oszacowanie dotyczy oszacowania częstotliwości okrągłego cylindra, czyli w ujęciu matematycznym wartości własnych dysku.
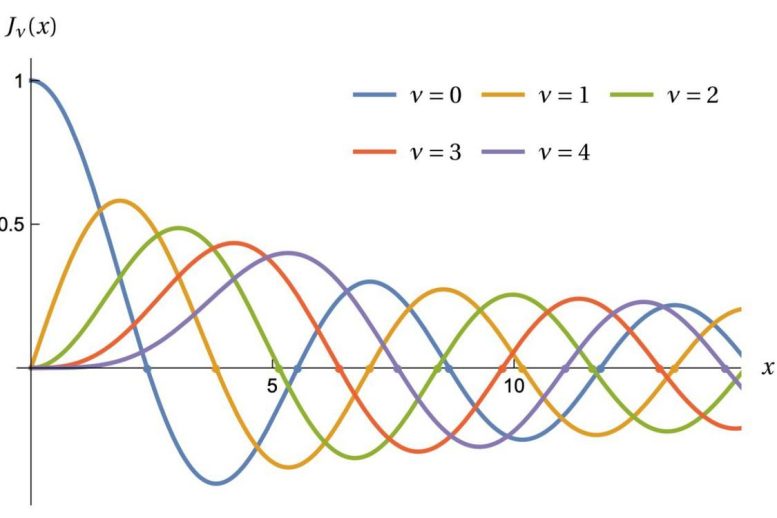
Ten diagram przedstawia funkcje Bessela, gdzie kropki odpowiadają częstotliwościom dźwięków wytwarzanych przez okrągły bęben. Źródło: Michael Levitin
Sam Polya potwierdził w 1961 roku swoje przypuszczenia dotyczące sfer tworzących płaszczyznę, takich jak trójkąty i prostokąty. Do ubiegłego roku przypuszczenie było znane tylko w tych przypadkach. Płyta, mimo pozornej prostoty, pozostała nieuchwytna.
„Wyobraźcie sobie nieskończoną podłogę pokrytą płytkami o tym samym kształcie, które pasują do siebie, aby wypełnić przestrzeń” – powiedział Poltrovic. „Można je układać w kwadraty lub trójkąty, ale nie w krążki. Dyski w rzeczywistości nie są dobrym kształtem do układania płytek.
Uniwersalność i wpływ matematyki
W artykule opublikowanym w lipcu 2023 roku w magazynie sportowym Wynalazki matematyczneNaukowcy wykazali, że przypuszczenia Bolyi są prawidłowe w przypadku dysku, a przypadek ten uznano za szczególnie trudny.
Chociaż ich wyniki mają głównie wartość teoretyczną, ich metoda dowodowa ma zastosowanie w matematyce obliczeniowej i obliczeniach numerycznych. Autorzy badają obecnie to podejście.

Józef Poltrovic
„Chociaż matematyka jest nauką podstawową, pod pewnymi względami jest podobna do sportu i sztuki” – powiedział Poltrovic.
„Próba udowodnienia ugruntowanej hipotezy to sport. Znalezienie eleganckiego rozwiązania to sztuka. W wielu przypadkach piękne odkrycia matematyczne są przydatne, wystarczy tylko znaleźć odpowiednie zastosowanie. „
Odniesienie: „Hipoteza polia dla sfer euklidesowych” Nikołaja Filonowa, Michaela Levitina, Iosifa Poltrovica i Davida A. Udostępnij, 5 czerwca 2023 r., Wynalazki matematyczne.
doi: 10.1007/s00222-023-01198-1
